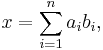Ring of integers

In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication. It is a commutative ring, and is the prototypical such by virtue of satisfying only those equations holding of all commutative rings with identity; indeed it is the initial commutative ring, as well as being the initial ring.

More generally the ring of integers of an algebraic number field K, often denoted by O_K (or 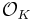), is the ring of algebraic integers contained in K.

Using this notation, we can write Z = O_Q since Z as above is the ring of integers of the field Q of rational numbers. And indeed, in algebraic number theory the elements of Z are often called the "rational integers" because of this.

An alternative term is maximal order, since the ring of integers of a number field is indeed the unique maximal order in the field.

The ring of integers O_K is a Z-module. Indeed it is a free Z-module, and thus has an integral basis, that is a basis b₁,...,b_n ∈ O_K of the Q-vector space K such that each element x in O_K can be uniquely represented as

with a_i ∈ Z. The rank n of O_K as a free Z-module is equal to the degree of K over Q.

The rings of integers in number fields are Dedekind domains.

Examples

If p is a prime, ζ is a pth root of unity and K=Q(ζ) is the corresponding cyclotomic field, then an integral basis of O_K=Z[ζ] is given by (1, ζ, ζ², ..., ζ^p−2).

If d is a square-free integer and K = Q(d ^1/2) is the corresponding quadratic field, then an integral basis of O_K is given by (1, (1 + d^1/2)/2) if d ≡ 1 (mod 4) and by (1, d ^1/2) if d ≡ 2 or 3 (mod 4).

The ring of p-adic integers Z_p is the ring of integers of a p-adic numbers Q_p.

See also

• Quadratic integer

References

• Neukirch, Jürgen (1999), Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften, 322, Berlin: Springer-Verlag, ISBN 978-3-540-65399-8, MR1697859